Choisissez la mise en page
Choisissez la police
Taille
Options d'impression
Bow Final No Key Points

Definitions
Kinetic Energy: is the capacity to do work to an objects motion
Variables: KE = (1/2)(mass)(velocity^2)
mass and velocity are inversely proportional. Meaning at a constant KE an increase in one (ie mass) would result in a decrease in the other (ie velocity). Due to this fact, velocity has a much greater effect on KE due to its power of 2/
Units: Nm or J (joules)
Strain Energy: is the capacity to do work due to the deformation of an object. It is a type of Potential Energy
Variables: SE = (1/2)(k)(x^2) where "k" is equal to the objects stiffness and "x" is equal to the deformation of the object. In this case the bend in the limbs of the bow.
k and x are also inversely proportional, with x (deformation) having a greater effect on SE
Units: Nm or J (joules)
Variables: KE = (1/2)(mass)(velocity^2)
mass and velocity are inversely proportional. Meaning at a constant KE an increase in one (ie mass) would result in a decrease in the other (ie velocity). Due to this fact, velocity has a much greater effect on KE due to its power of 2/
Units: Nm or J (joules)
Strain Energy: is the capacity to do work due to the deformation of an object. It is a type of Potential Energy
Variables: SE = (1/2)(k)(x^2) where "k" is equal to the objects stiffness and "x" is equal to the deformation of the object. In this case the bend in the limbs of the bow.
k and x are also inversely proportional, with x (deformation) having a greater effect on SE
Units: Nm or J (joules)

Draw 1 Strain Energy Conceptualized
With the string attached to the bow we reference of the strings angle from the connection between the string and arrow to the ends of each limb as 180 degrees. From here drawing back the string decreases this angle creating bend on the limbs of the bow and the storing/creation of strain energy.
The closer this angle is to the resting angle of 180 degrees the less strain on the limbs of the bow meaning less strain energy (potential energy) stored.
The closer this angle is to the resting angle of 180 degrees the less strain on the limbs of the bow meaning less strain energy (potential energy) stored.

Variables for Loose 1
Here we see the distance traveled by the arrow ( 14.41 meters) and the amount of time (0.433 seconds) it took the arrow to travel that distance.
With these we can find the velocity of the arrow.
We also have the mass of the arrow to be 0.0185 kgs
With these we can find the velocity of the arrow.
We also have the mass of the arrow to be 0.0185 kgs

Kinetic Energy Loose 1
By taking the distance traveled by the arrow and dividing it by the time we get its velocity.
The mass of the arrow is 0.0185 kg
With these two variables we can find the Kinetic Energy of the arrow during its "max" velocity in flight
Kinetic Energy = (1/2)(mass)(velocity^2)
KE = (1/2)(0.0185kg)(33.20(m/s)^2)
KE = 10.20 J
The mass of the arrow is 0.0185 kg
With these two variables we can find the Kinetic Energy of the arrow during its "max" velocity in flight
Kinetic Energy = (1/2)(mass)(velocity^2)
KE = (1/2)(0.0185kg)(33.20(m/s)^2)
KE = 10.20 J

Strain Energy Draw 1
Since the Strain Energy stored in the bow (as potential energy) is transfered from the bow to the arrow into Kinetic Energy we can assume the Strain Energy to also be 10.20 J
We have found the Stiffness of the bow (k = 342 Nm) (Kooi, B., 1998, p. 724).
We can now find the deformation of the bow
10.20 J = (1/2)(342Nm)(x^2)
x = square root of [(10.20 J)/[(1/2)(342 Nm)]]
deformation = 0.173
We have found the Stiffness of the bow (k = 342 Nm) (Kooi, B., 1998, p. 724).
We can now find the deformation of the bow
10.20 J = (1/2)(342Nm)(x^2)
x = square root of [(10.20 J)/[(1/2)(342 Nm)]]
deformation = 0.173

Draw 2 Strain Energy Conceptualized
Since we have concluded that the closer the angle is to 180 degrees there will be less strain on the limbs of the bow thus creating less stored strain energy. In draw two the bowstring is pulled back slightly farth creating a lesser angle of the string between the arrow and the limbs of the bow. This creates a much greater bend on the limbs and as a result greater storage of energy, Strain Energy.
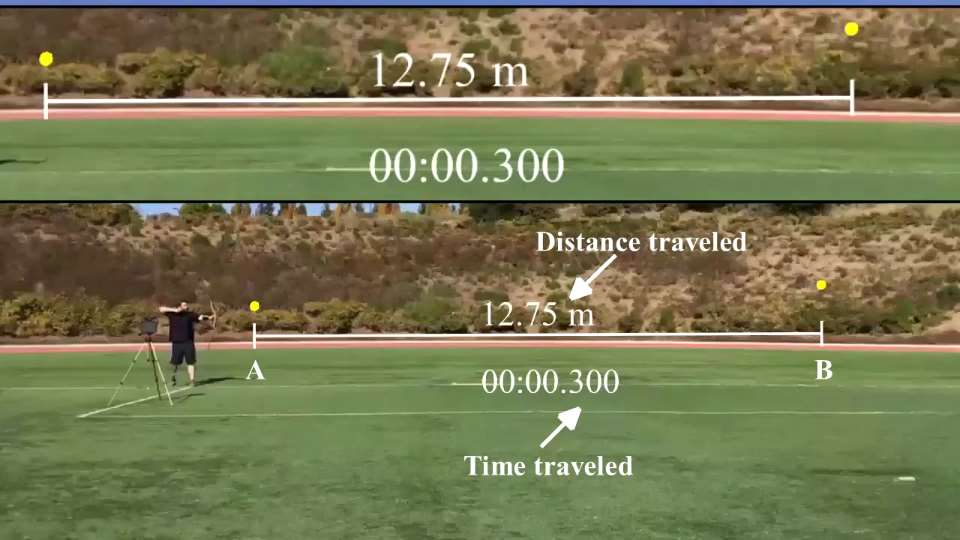
Variables for Loose 2
Here we see the distance traveled by the arrow ( 12.75 meters) and the amount of time (0.300 seconds) it took the arrow to travel that distance.
With these we can find the velocity of the arrow.
Again, the mass of the arrow is 0.0185 kgs
With these we can find the velocity of the arrow.
Again, the mass of the arrow is 0.0185 kgs

Kinetic Energy Loose 2
By taking the distance traveled by the arrow and dividing it by the time we get its velocity.
The mass of the arrow is 0.0185 kg
With these two variables we can find the Kinetic Energy of the arrow during its "max" velocity in flight
Kinetic Energy = (1/2)(mass)(velocity^2)
KE = (1/2)(0.0185kg)(42.50(m/s)^2)
KE = 16.71 J
The mass of the arrow is 0.0185 kg
With these two variables we can find the Kinetic Energy of the arrow during its "max" velocity in flight
Kinetic Energy = (1/2)(mass)(velocity^2)
KE = (1/2)(0.0185kg)(42.50(m/s)^2)
KE = 16.71 J

Strain Energy Draw 2
Again, since the Strain Energy stored in the bow (as potential energy) is transfered from the bow to the arrow into Kinetic Energy we can assume the Strain Energy to also be 16.71 J
We have found the Stiffness of the bow (k = 342 Nm) (Kooi, B., 1998, p. 724).
We can now find the deformation of the bow
16.71 J = (1/2)(342Nm)(x^2)
x = square root of [(16.71 J)/[(1/2)(342 Nm)]]
deformation = 0.221
We have found the Stiffness of the bow (k = 342 Nm) (Kooi, B., 1998, p. 724).
We can now find the deformation of the bow
16.71 J = (1/2)(342Nm)(x^2)
x = square root of [(16.71 J)/[(1/2)(342 Nm)]]
deformation = 0.221

References
Kooi, B. (1998). Bow-arrow interaction in archery. Journal of Sports Sciences, 16(8), 721-731.
Yingling, V. (2019). Lecture Slides. Work-Energy-Power
Yingling, V. (2019). Lecture Slides. Work-Energy-Power
powered by
dartfish.tv
The Relationship Between Kinetic and Potential Energy
In this video we learn the concepts of kinetic energy as well as potential energy in the form of strain energy. We anylyze the interactions between a bow, its string and the arrow to help us learn these concepts.
Biomechanical Concepts -
Energy
Biomechanical Concepts -
Energy -
Kinetic Energy
Biomechanical Concepts -
Energy -
Potential Energy
