Layout wählen
Schrift wählen
Größe
Druckoptionen
Open
The Breakdown
SBS throw timed

Impulse
Describe Impulse Here & Compare throwing Mechanics
Impulse = Force (F) * time (t) [Newton*sec]
Talk about follow through: By increasing the overall follow through for throwing the ball, the time that the force is applied to the ball increases. In comparison, a short arm throw has a lower time. The decrease in "t" would demand a higher force "F" to be applied to the ball in order to maintain the same impulse and affect the momentum of the ball equally.
The time can be further increased by allowing more follow through of the wrist at the end of the action.
Impulse = Force (F) * time (t) [Newton*sec]
Talk about follow through: By increasing the overall follow through for throwing the ball, the time that the force is applied to the ball increases. In comparison, a short arm throw has a lower time. The decrease in "t" would demand a higher force "F" to be applied to the ball in order to maintain the same impulse and affect the momentum of the ball equally.
The time can be further increased by allowing more follow through of the wrist at the end of the action.

Comparison
Rotation of the upper torso about the longitudinal axis allows for increased time to apply force. The short-arm motion ends abruptly and takes less time to complete.
Projectile Motion

Release Point: Projection Angle
Factors that determine the trajectory of the projectile object:
PROJECTION ANGLE
The angle of the object at the point of take-off. The optimal angle is dictated by the objective of the action. Assuming constant velocity(negligible air resistance), an angle greater than 45° results in greater projectile range(horizontal distance traveled). Displayed is a projection of 36.0°, less than 45°, resulting in less range and shorter flight time
PROJECTION ANGLE
The angle of the object at the point of take-off. The optimal angle is dictated by the objective of the action. Assuming constant velocity(negligible air resistance), an angle greater than 45° results in greater projectile range(horizontal distance traveled). Displayed is a projection of 36.0°, less than 45°, resulting in less range and shorter flight time
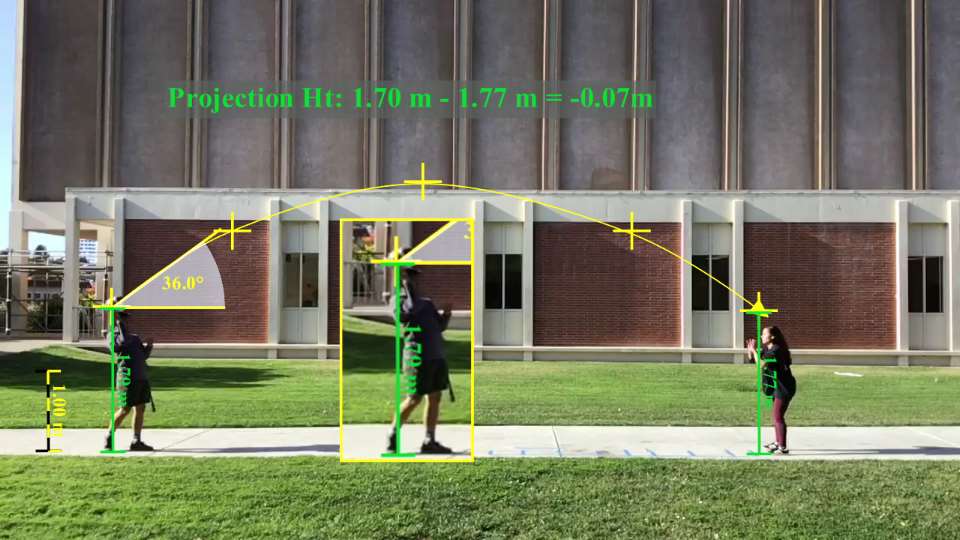
Release Point: Projection Height
Factors that determine the trajectory of the projectile object:
Projection Height: the projection height of the object is the difference between the height of the object at take off and the height of the projectile at the objective point (in this case, the position where the football is caught).
Projection Height: the projection height of the object is the difference between the height of the object at take off and the height of the projectile at the objective point (in this case, the position where the football is caught).
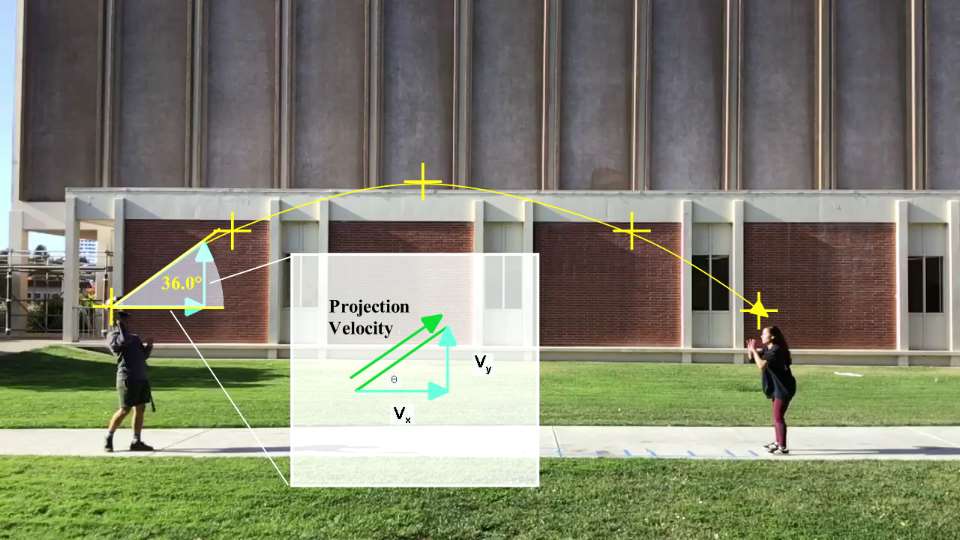
Release Point: Projection Velocity
Factors that determine the trajectory of the projectile object:
Projection velocity determines maximum height and length of trajectory, provided all other factors are constant. Projection velocity has a vertical component (Vy) and a horizontal component (Vx). To find both components of the projection velocity:
Vy = Proj. Velocity * sin Proj. θ
Vx = Proj. Velocity * cos Proj. θ
Projection velocity determines maximum height and length of trajectory, provided all other factors are constant. Projection velocity has a vertical component (Vy) and a horizontal component (Vx). To find both components of the projection velocity:
Vy = Proj. Velocity * sin Proj. θ
Vx = Proj. Velocity * cos Proj. θ
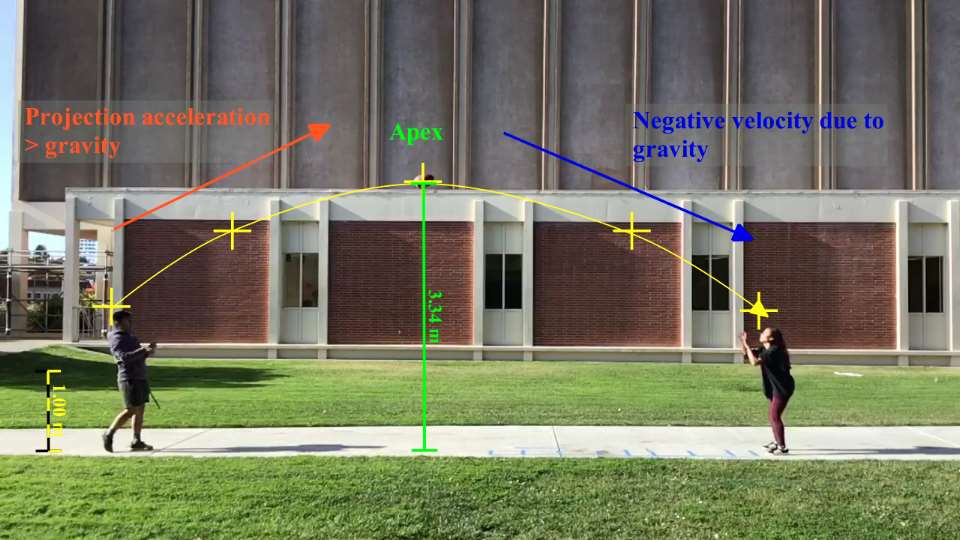
Apex
The maximum height the object can reach is termed the apex of the projectile. The apex can be found at the hightest point of the parabolic path that the projectile travels.
At the apex, the vertical velocity of the projectile equals 0. This is the point where the acceleration due to gravity has brought the vertical velocity to zero, and the remainder of the path travelled by the projectile is due to negative velocity.
At the apex, the vertical velocity of the projectile equals 0. This is the point where the acceleration due to gravity has brought the vertical velocity to zero, and the remainder of the path travelled by the projectile is due to negative velocity.

Range
The range is defined by the horizontal distance travelled by the projectile from the point of release to the point of landing.
Impulse 2 - Catch Comparison

Catch Comparison
In order to decrease the force applied to the receiver, the catch can be changed to increase the time. The diamond form for the hand position is optimal for completing a catch, but football players typically play with gloves (which increase the "t" of the catching impulse). In a less competitive scenario, to decrease the force of impact, increasing the time of the reception can be performed, providing "give," for the receiver.
END
powered by
dartfish.tv
Impulse & Projectile Motion
Impulse & projectile motion described and displayed in the context of passing and receiving a football. Two styles are displayed, and the factors that affect the trajectory of the ball are detailed in key positions.
Biomechanical Concepts -
Projectile Motion
