Choose layout
Choose font
Size
Print options
Backflips: Conservation of Angular Momentum

The significance of the "tuck"
The image on the right shows how the tuck increases angular velocity by decreasing the moment of inertia. A non-tucked position would result in a greater inertia and a decrease in angular velocity. Angular momentum stays constant once I jump and lose contact with the ground. You will see in a bit the results of a tucked and non-tucked backflip.
DISTRIBUTION OF MASS IS KEY DURING AN ANGULAR/ROTATIONAL MOTION!!!
DISTRIBUTION OF MASS IS KEY DURING AN ANGULAR/ROTATIONAL MOTION!!!
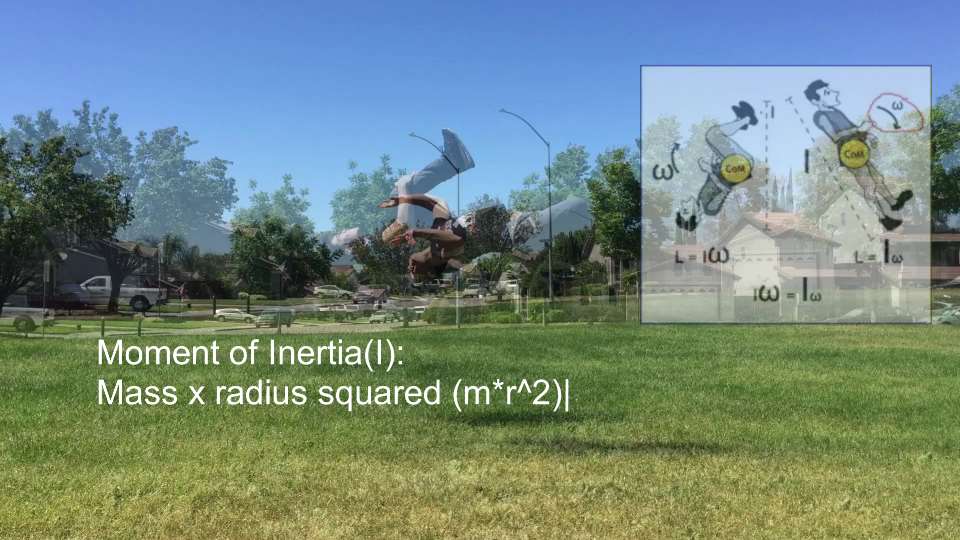
Moment of Inertia
In order to flip over and land on my feet I need to increase my angular velocity. This will be accomplished by decreasing my moment of Inertia. I can't alter my mass during the flip but I do have the ability to change my radius by "tucking".
Backflip with tuck
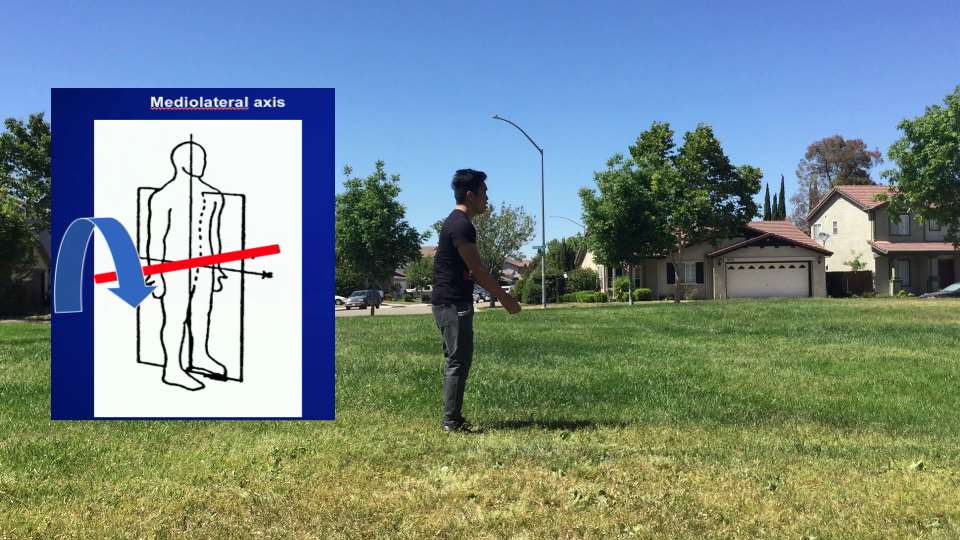
Center of rotation: Mediolateral Axis
The mediolateral axis impales the body from side to side. It acts as the center of rotation during a backflip (the body rotates in the mediolateral axis during a backflip/frontflip motion). With the mediolateral axis as the center of rotation, we have a big moment of inertia (the center of rotation to our head/center of rotation to our feet).

Mass and radius
I weigh 154.5 pounds so 154.5lb*1kg/2.2046= 70kg
I used my height (the diameter in this case) as a reference point in order to obtain the radius, which is 1.68m from head to toe.
I used my height (the diameter in this case) as a reference point in order to obtain the radius, which is 1.68m from head to toe.

Fundamental Movement Pattern 1
The squat/lift is a fundamental movement pattern necessary for the prepration phase for the jumping portion of the backflip motion.

Moment of Inertia: Tuck
I= 70kg*(0.68m)^2
= 32.37kg. m^2
A decrease in Moment of Inertia about the mediolateral axis resulting in an increase in angular velocity. The end result is me landing on my feet
= 32.37kg. m^2
A decrease in Moment of Inertia about the mediolateral axis resulting in an increase in angular velocity. The end result is me landing on my feet
Backflip with no tuck

Moment of Inertia: No tuck
I= 70kg*(0.91m)^2
= 57.96kg. m^2
A increase in Moment of Inertia about the mediolateral axis resulting in a decrease in angular velocity. The end result is me landing on my stomache. There was not enough angular velocity to get me all the way through the backflip in order for me to land on my feet.
= 57.96kg. m^2
A increase in Moment of Inertia about the mediolateral axis resulting in a decrease in angular velocity. The end result is me landing on my stomache. There was not enough angular velocity to get me all the way through the backflip in order for me to land on my feet.
powered by
dartfish.tv
Video 4: Conservation of Angular Momentum
In this video I will be demonstrating the conservation of Angular Momentum with two backflips. The video will reveal the significance of “tucking” when doing a backflip. With angular momentum equaling moment of inertia times angular velocity (Angular momentum = I*ω), I will manipulate the angular velocity by manipulating my moment of inertia (I = m*r²). This will be done by increasing or decreasing my radius, which is accomplished by whether or not I tuck during the backflip. One backflip will initiate the tucking sequence while the other will not. Once I jump and leave the ground the angular momentum stays constant. I will be manipulating my moment of inertia which would either increase or decrease my angular velocity.
When gravity is the only force acting on the object you have a conservation of angular momentum.
Angular Momentum = I*ω
ω = Angular velocity
I = Moment of Inertia
I = m*r²
• Mass (m): An increase in mass results in an increase in the moment of inertia. Doubling the mass (m) will double the moment of inertia.
• Radius (r): Represents the distribution of mass. Doubling the radius (r) will quadruple the moment of inertia.
So, for Rotation/Angular motion: Distribution of mass is key.
When gravity is the only force acting on the object you have a conservation of angular momentum.
Angular Momentum = I*ω
ω = Angular velocity
I = Moment of Inertia
I = m*r²
• Mass (m): An increase in mass results in an increase in the moment of inertia. Doubling the mass (m) will double the moment of inertia.
• Radius (r): Represents the distribution of mass. Doubling the radius (r) will quadruple the moment of inertia.
So, for Rotation/Angular motion: Distribution of mass is key.
Biomechanical Concepts -
Kinematics
Biomechanical Concepts -
Kinematics -
Angular Kinematics
